Silverman's game
In game theory, Silverman's game is a zero sum game played on the unit square. It is named for David Silverman.
It is played by two players on a given set S of positive real numbers. Before play starts, a threshold  and penalty
and penalty  are chosen with
are chosen with 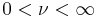 and 1 < T < ∞ Each player chooses an element of S. Without loss of generality, suppose player A plays x and player B plays y, with x > y. Then the payoff to A is 1 if 1 < x/y < T and
and 1 < T < ∞ Each player chooses an element of S. Without loss of generality, suppose player A plays x and player B plays y, with x > y. Then the payoff to A is 1 if 1 < x/y < T and 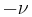 if x/y > T; equal numbers involve zero payoff. Thus each player seeks to choose the larger number but, provided
if x/y > T; equal numbers involve zero payoff. Thus each player seeks to choose the larger number but, provided 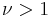 , there is a penalty of
, there is a penalty of  for choosing too large a number.
for choosing too large a number.
References
- R. J. Evans 1979. Silverman's game on intervals. American Mathematical Monthly, volume 86, number 4, pp. 277–281.